Copyright © 1999. Mirametrics, Inc. All Rights Reserved.
Overview
An important step in CCD image calibration is the removal of the thermal signature commonly known as "dark count". An accurate measurement of the dark count in a CCD image cannot be made from the image itself. To determine the dark count, a time exposure is taken with the camera shutter closed to produce an image containing the thermal signature of the CCD chip. This "dark frame" is then subtracted from the "normal" data image of same exposure to remove the thermal signature present in the data image.
Dark count is the product of a "dark current", or rate per second of electrons created by the CCD, and the exposure time in seconds. Thus the amount of dark count present in a CCD image depends on the temperature of the CCD chip. In fact, the dark current is slightly different for each pixel of the CCD. The dark current varies with temperature by a complex mathematical relationship. To remove the thermal signature, a dark frame must accurately estimate the dark count unique to each pixel of the image. If the temperature of the CCD when the dark frame is taken is different from the temperature of the CCD chip when the normal light frame is taken, then the wrong amount of dark count is removed, giving a poor correction for the thermal signature of the CCD. It is not just an issue of how the CCD temperature fluctuates over a timescale of minutes but, more critically, the CCD temperature now compared with 2 hours ago when dark frames were taken. The importance of temperature stability is two fold:
- The dark current distribution has more than 1 population of values, each with its own temperature scaling law. The hotter populations, while comprising at most a few percent of the total, are even more sensitive to temperature variations than the results shown here. They subtract very poorly when temperature variations are present, leaving a residual sprinkling of bright and dark points over the image.
- Proper flat field correction depends upon accurate dark count removal. An error in the dark count reveals itself as a "convex" or "concave" appearing image instead of a constant one after flat field correction.
Longer exposure times, employed in astronomy and other low light imaging applications, exacerbate the variations in dark count. This Tech Note shows how temperature differences between the dark frame and light frame affect the dark count correction in CCD data.
Numerical Models
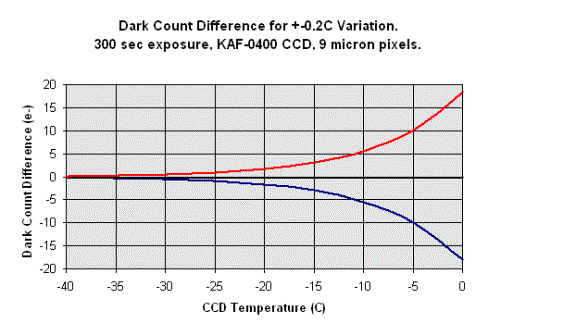
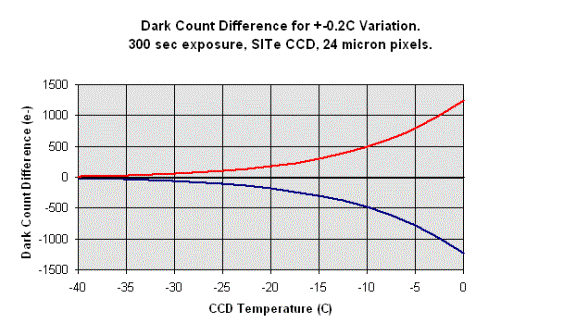
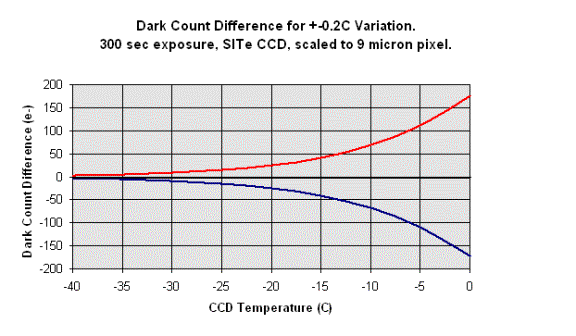
The graphs below show the results of numeric models that calculate the dark count as a function of CCD temperature. Only the majority population of pixels is considered. The minority populations having 5, 10, 50, or more times the average dark current are not considered. Calculations were made for a Kodak KAF-0400 CCD, which has 9 micron pixels, and the SITe Si-502a CCD, which has 24 micron pixels. The Kodak models assumed a simple power law relationship with a "doubling temperature" of 5.8C. For the SITe CCD, the dark current was calculated using an exact mathematical expression that is combination of a power law and other terms. The SITe calculations per pixel were scaled down by a factor of 7.11 times to correct its larger pixel area to that of the Kodak CCD. The scaled SITe results are more directly applicable to the Kodak results, since the important quantity is not the amount of dark count per pixel, but rather the amount of dark current per unit area under an image detail appearing in the CCD frame.
The top figure below shows the model calculations for the Kodak KAF-0400 CCD. The second figure shows model calculations for the SITe Si-502a CCD chip scaled to 9 micron pixels. The SITe chip clearly has larger dark current at a given temperature, so it also has more sensitivity to temperature variations. Each graph below has two curves that define the dark current when the CCD is 0.2C warmer than average and 0.2C cooler than average. The dark count is given in units of electrons (e-). A point on a red curve indicates that the dark count is higher by that number of e- if the CCD temperature is 0.2C warmer than expected. The blue curves handle the converse case for the CCD being 0.2C colder than expected. The curves show the amount of error that would result from subtracting a dark frame taken 0.2C warmer or cooler than the CCD when the light exposure was taken. The difference 0.2C is based on the industry standard adoption of 0.1C rms temperature variation as a performance spec for CCD cameras. Therefore, one might find that the dark frame was taken when the CCD was 0.1C warmer than average, and the data frame was taken when the CCD was 0.1C cooler than average, creating a 0.2C difference in dark count. The curvature in these relationships results from the power law relationship between dark current and temperature. >
To first order, the results given here can be applied to larger temperature variations by simply scaling the result by the temperature difference. For example, to estimate the effect of 2.0C difference, multiply the graphical value by 2.0 / 0.2 = 10 times.
Discussion
Comparing the two models shows some interesting results. Most obvious is the difference in the magnitude of the dark count error for the two different chips. The SITe CCD is optimized differently than the Kodak CCD, and this results in a higher dark current at a given temperature. Higher dark current is not a "defect" of the SITe chip design, but it simply means that the chip must be operated cooler than a Kodak chip to give comparable dark current. Both are excellent CCD's in their niche of operation. The CCD temperature must also be very stable if good correction of the thermal signature is to be attained. CCD temperature controllers are only so good, and they cannot maintain the temperature at a perfectly constant level. The question then is how stable is "stable enough". Since the error decreases as the dark current decreases, it is obvious why CCD's are cooled to cryogenic temperatures for making the most critical measurements. There is always going to be variation in the CCD temperature during an imaging session---the issue is the amount of "damage" done by a given level of stability. Clearly, the colder the CCD, the better.
Clearly, the best image calibration is achieved when there is zero difference in CCD temperature when data frames and dark frames are taken. However, in the real world, CCD cameras differ in the accuracy and stability of their temperature control systems. Bear in mind that the criterion "0.1C RMS" is a 1-sigma statistical quantity. This does not mean that the CCD temperature varies within limits of +-0.1C, but that 68% of the time the temperature held is within 0.1 degree of the nominal value and 95% of the time it is within 2-sigmas, or 0.2C of the nominal value. But even tight temperature control doesn't guarantee that the temperature is accurately measured. Even more important is not just that the temperature control believes it is stable within a fraction of a degree, but that the temperature controller accurately measures the actual CCD temperature. To do this with thermoelectrically cooled cameras, a simple temperature control circuit measures temperature relative to an ambient temperature sample. In a laboratory environment, where the ambient room temperature is stable, temperature control is not a complex problem. In applications such as astronomy, in which the camera is subjected to the changing temperature of the night, a more sophisticated control loop is needed because it must compensate for the variation in ambient temperature near the camera. The most critical CCD work requires that both concerns be satisfied:
- The CCD temperature must be accurately measured.
- The temperature remains stable over time.
Both problems are partially compensated simply by cooling the CCD as much as possible to minimize both the dark current and its variation.