Author: Michael Newberry, Ph.D., Mirametrics, Inc.
Overview
Centroid noise is a random error, or "noise" component of a photometric measurement that results from placement of the measuring aperture on the object being measured. Centroid noise is not widely known as part of the internal error for a photometric measurement. In this Tech Note, I will examine the effect of centroid noise on stellar photometry. This study uses a series of repeated measurements of the same object to show the effect of centroid noise. The software used was Mira Pro, but the identical algorithms are used in all Mira platforms.
A photometric measurement involves measuring two quantities:
- The total signal is summed inside an aperture of a specified size, centered on the object.
- The background signal is estimated underneath the object. In aperture photometry, it is calculated using the pixels inside a ring (or annulus) concentric with the object.
The brightness of the object is given simply as the difference "total - sky", or (1) - (2). The trick in doing good photometry is how to calculate both "object+sky" and "sky" measures robustly in the presence of background variations, nearby objects, bad pixels, under-sampling, and other factors. But in addition, the measurement of the object signal depends upon how the aperture is centered on the object. Especially for faint stars, the centroid position of the object is itself subject to some uncertainty, which translates into different parts of the star profile being measured, and thence into a different magnitude measurement. Even small differences in placement of the aperture add to the uncertainty of the photometric measurement. This uncertainty will not be known from a single measurement but will appear when different measurements are compared using the error estimate from each measurement.
The Nature of Centroid Noise
The position of an object is computed using the intensity of pixels. The centroid position is a weighted average position (i.e., a type of "center of mass" of the star profile), but the weighting scheme varies among different techniques; some methods are more accurate than others. Even using a "good method", nature provides a limiting precision with which a centroid can be computed. Since the centroid is computed from pixel values and each pixel has random noise (you do not know its "true" value), this makes the centroid position uncertain to some degree. Mira has a very good centroid algorithm, but the centroid value still has some amount of uncertainty. Moreover, the fainter the star, the less certain the centroid position. This results because the relative uncertainty in pixel value increases as the signal decreases. In other words, the contribution of centroid noise is magnitude dependent and becomes greater for fainter objects.
The crux of the problem is this: How do you get a handle on the amount of centroid noise inherent in your photometric measurements? There are 2 ways to do this:
- Pick a star and repeat the magnitude measurement by randomly displacing the measuring aperture in all directions by some small amount. The small amount should correspond to what you believe to be the uncertainty in the centroid position. This is difficult to know and this is a limitation of this method.
- Take many frames of the same star under identical conditions and at the same airmass (or almost the same airmass), then measure the signal from the star on each frame. Compare the measurements and their random errors. The errors will almost always be significantly larger than the internal errors estimated from measuring on a single image.
Centroid noise can become an issue when apertures are placed manually onto new objects, as would be done using the "move" mode from the Mira photometry toolbar. If the target object is a point source, it is usually better to use the centroid button after manually moving the aperture in order to minimize the contribution of centroid noise.
Numerical Simulation
How large an effect is centroid noise? To address
this issue, a simple numerical simulation was used to
answer the following question: If we wobble around the
measuring aperture by a small amount, how much does that
translate into the random error of the magnitude
measurement? Using a single image, the brightness of a star was repeatedly measured
using apertures placed at slightly different positions.
This simulates the effect of random deviations in the
centroid positions caused by pixel noise in different
images.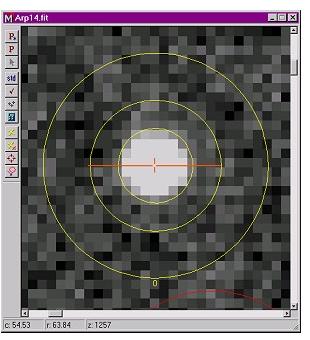
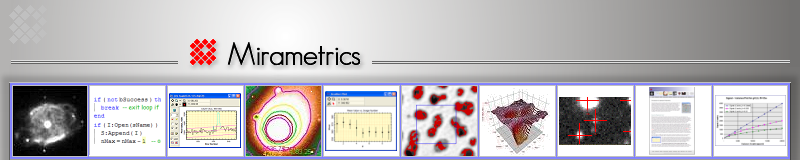
To move the apertures, the auto-centroid flag was disabled so that the measurement would be made at the literally marked position rather than at the centroid position. Then Mira was used in "move mode" by clicking the move button on the photometry toolbar. Each time the aperture was dropped at a new position, Mira reported the new measurement. These measurements were tallied and listed in the table below. The target star has a net count, or "volume", of 6343 counts above background. This corresponds to an internal error of ~0.01 magnitude. The figure at left shows a Mira image window centered on the target star. The image was magnified 16 times to allow the aperture to be placed at fractional pixel offsets. Note that the contrast was also stretched to show where the star merges into the background. In typical photometric measurements, the object aperture would enclose about the amount of the star profile shown here, or perhaps a bit less. While a smaller aperture can give higher S/N on faint stars (because less sky noise is included in the measuring aperture), a smaller aperture increases the amount of centroid noise. The two effects compensate each other to some degree. Also notice the partially sampled pixels around the rim of the star measuring aperture. Mira uses an exact calculation of partial pixel contributions. Without that, the centroid noise would be far higher.
The second figure shows a horizontal intensity cut through the star as marked by the orange image cursor in the figure above. The column range of the plot corresponds to the width of the inner background aperture. The repeat measurements are shown in the table below. The bottom 2 rows of the table give the mean and standard deviation of the magnitude, column, and row position. The variation in centroid
position given by the standard deviation is ~0.2 pixels.
As shown in the table, jittering the measuring apertures by
this small amount leads to a variation in the measured
brightness of 0.005 magnitude. The centroid noise is approximately
1/2 the computed error of the measurement! It is important to appreciate that
centroid noise is an external error
and is not calculated as part of the magnitude error,
which is purely an internal error based on photon
statistics and camera characteristics. Clearly, doing
high-precision photometry means not only using the best
photometric algorithms but also using the best
centroid algorithms.
| Trial | Magnitude | Column | Row |
| 1 | 14.937 | 54.658 | 63.850 |
| 2 | 14.932 | 55.031 | 63.844 |
|
3 |
14.948 |
55.094 |
64.281 |
|
4 |
14.937 |
54.656 |
63.969 |
|
5 |
14.932 |
54.969 |
63.969 |
|
6 |
14.937 |
54.719 |
63.594 |
|
7 |
14.939 |
54.594 |
64.094 |
|
8 |
14.943 |
54.844 |
64.281 |
|
9 |
14.939 |
54.906 |
63.969 |
|
10 |
14.930 |
54.906 |
63.906 |
|
11 |
14.938 |
54.594 |
64.031 |
|
12 |
14.936 |
54.656 |
63.719 |
|
13 |
14.937 |
54.719 |
63.531 |
|
14 |
14.936 |
54.406 |
63.656 |
|
Mean |
14.937 |
54.768 |
63.907 |
|
Std Dev |
0.005 |
0.195 |
0.230 |
Conclusions
I have shown that Centroid Noise is a significant part of the photometric error budget. Unfortunately it cannot be determined from a single image. The tests performed here showed a 0.005 magnitude random error attributable only to random misplacement of the aperture by 0.2 pixels RMS about the true center of the object. Although the centroid uncertainty is far less than 0.2 pixels for a bright star, it can easily be this large or larger for faint stars. Centroid noise would appear as external error which increases the scatter between measurements relative to the scatter predicted by their error bars that are based on internal noise sources.
When doing high-precision aperture photometry, seeking to achieve measurement uncertainties near, or below 0.01 magnitude, one must concerned about the effects of centroid noise. The only way to minimize centroid noise is by using a robust, high precision centroid algorithm for determining the placement of the object measuring aperture.