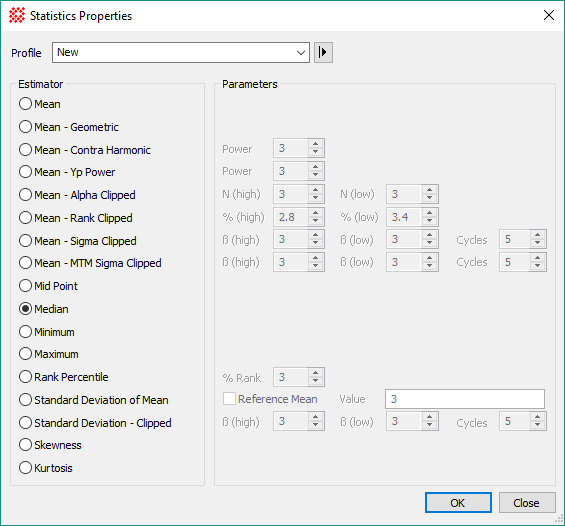
Properties of the Statistics Properties dialog

Mean

Calculates the simple average with no weighting or rejection of bad values.

Mean - Geometric

Calculates the geometric mean, which is a mean value weighted by the reciprocal of the individual values.

Mean - Contra Harmonic

Calculates the weighted harmonic mean value in which each weight involves the value raised to the p power.

Mean - Yp Power

Calculates the weighted mean value in which the weight is given by the exponent "p", which is the value raised to the p power.

Mean - Alpha Clipped

Calculates a clipped mean in which a specified number N(high) and N(low) values are excluded from the sample.

Mean - Rank Clipped

Calculates a clipped mean in which the specified percentiles %(high) and %(low) of values are excluded from the sample.

Mean - Sigma Clipped

Calculates a clipped mean in which values are rejected if more deviant than ß(high) and ß(low) above and below the sample distribution mean. Refinement of the calculated mean value is repeated up to specified maximum number of cycles. Use this method when calculating the mean value in the presence of deviant values that are outliers from a Normal distribution.

Mean - MTM Sigma Clipped

Calculates a clipped mean in which values are rejected if more deviant than ß(high) and ß(low) above and below the sample distribution estimator. This computation includes both the mean and median values of the sample distribution. Refinement of the calculated mean value is repeated up to specified maximum number of cycles. Use this method when calculating the mean value in the presence of deviant values that are outliers from a Normal distribution.

Mid Point

Calculates the midpoint between the sample minimum and maximum values.

Median

Calculates the sample median (50th percentile).

Minimum

Calculates the minimum values of the sample.

Median

Calculates the maximum values of the sample.

Rank Percentile

Calculates the ranked percentile value based on the %Rank parameter. For example, if %rank = 50, then the 50th percentile, or median, value is returned.

Standard Deviation of Mean

Calculates the Standard Deviation about the mean value. To calculate the standard deviation about a specific mean value, check the Reference Mean box and enter the target mean value. Otherwise, the ordinary standard deviation is calculated.

Standard Deviation - Clipped

Calculates the Standard Deviation in which values are rejected if more deviant than ß(high) and ß(low) above and below the sample distribution mean. Refinement of the calculated mean value is repeated up to specified maximum number of cycles. Use this method when calculating the standard deviation in the presence of deviant values that are outliers from a Normal distribution.

Skewness

Calculates the statistical skewness which characterizes the asymmetry of the sample distribution. Skewness greater than 0 indicates a positive bias and skewness less than 0 indicates a negative bias.

Kurtosis

Calculates the relative weight of central values to tail values in the sample distribution. The value is adjusted to a reference value of 0 for the Normal distribution. Kurtosis greater than 0 indicates that the distribution is taller than a Normal distribution (too narrow, or "leptokurtic") while a value less than 0 indicates the distribution is flatter than a Normal distribution (flatter, or "platykurtic"). By definition, the Normal distribution has the reference ratio of central area to tail area, and is called "mesokurtic".