Magnitude Calculations
This topic describes how the Aperture Photometry
package calculates the magnitudes and their random errors (or
"uncertainties"). These quantities, as related to the table of
photometry results, are also described in the topics Photometric
Measurement Definitions and Photometric Error
Definitions. This topic describes the math behind the
calculations and how apertures are measured on an image.
Calculating the Magnitude
Mira computes the magnitude as
m = K – 2.5 log (
Net Flux )
where
-
K is the photometric "zero point".
-
Net Count = Total Object Aperture Count -
Average Background Count * Object Area.
-
Net Flux = Net Count * Gain / Exptime.
-
Object Area is the area of the circular or
elliptical object aperture.
Here are some addition remarks about the quantities
listed above:
-
The Net Count is
simply the total count inside the object aperture minus the
background value inside the object aperture. Since the background
value inside the object aperture cannot be determined, it must be
estimated from pixels nearby.
-
The Total Object Aperture
Count is the sum of all pixel values inside the object
aperture, i.e., the sum of the object signal inside the object
aperture plus the background signal inside the object
aperture. Mira determines the background from pixels inside a
concentric annulus formed by two rings located beyond the point
where the star profile merges into the background noise. This is
listed in the photometry output (measurement table or text editor)
in the column labeled Ap Sum. This
value may be used to manually calculate the magnitude using an
alternative nearby background value, such as when the background
annulus contains a very bright star.
-
The Average Background
Count is listed in the photometry output in the column
labeled Backgr. It is in units of
counts.
-
The Object Area is
calculated as described near the end of this topic.
The camera gain ("Gain") and exposure time ("Exptime") are obtained from the FITS keywords GAIN
and EXPTIME. The Total
Count,Net Count, and
Background Count are measured in raw
pixel value units (often called DN or ADUs"). The Net Flux therefore represents the total number of
electrons per second attributable to the object, above the
sky.
To compute the Flux, the image signal is summed
over all pixels inside all whole and partial pixels inside the
innermost "object" aperture (see below). From this sum is
subtracted the estimated sky count computed from pixels in the
annulus between the 2 outer apertures. If the GAIN and EXPTIME
keywords are not present in the image header, or they are wrong,
you can add them or edit them using the Image
Information page of the Aperture
Photometry Properties dialog. Also see the topic Fixing Header
Problems in Photometric Data. You can also change the names
used for fetching the GAIN, EXPTIME, and RDNOISE values using the
Photometry
Keywords dialog.
The value K is the
photometric zero point. The zero point is assumed to be 0 or the
value of the ZERO-PT keyword in the image header. If the value is
0, then the magnitude may be called a "raw magnitude". If a zero
point value is computed for a particular instrumental setup and
used in the calculation, the result is called "instrumental
magnitude". If the zero point value, K, is unknown, it may be
calculated using standard stars of known magnitude.
Magnitude Errors
The uncertainty of the magnitude measurement is
calculated in two ways: an empirical error, listed in the Report
Window as Error, and a theoretical
value listed asError(T) . The
reported values may or may not include the uncertainty in the
photometric zero point, which is calculated when more than 1
standard star is used. This option is controlled by theInclude Zero Point Error check box on the
Other
Properties page. If checked, the reported error is the Root Sum
Square ("RSS") value of the internal error of the measurement and
the error of the mean of the zero point. The latter value is
reported in the Photometry Measurements.
The empirical error involves the noise measured in
the sky annulus as well as the values of GAIN, RDNOISE, and EXPTIME
from the image header. The theoretical error uses the keywords but
not the measured sky noise. The theoretical error estimate is the
minimum possible uncertainty that could be measured at a given
magnitude. You can change the values of GAIN, EXPTIME, and RDNOISE
on the Image Information page. Doing so will change the
error values by a small amount.
Description of the Apertures
The aperture photometry procedure uses 3 apertures
to measure an object:
-
The central aperture measures the total signal
for the object. It does not have to enclose 100% of the signal from
the object, provided that all objects in the image are measured
using the object same aperture shape and size. The total count
inside the object aperture is listed as the Ap
Sum quantity in the photometry output (measurements table or
text editor).
-
The outer 2 apertures form a concentric ring, or
annulus where the local sky (background) is measured. This is
subtracted from the total signal inside the object aperture to
produce theNet Count listed in the
photometry output (measurements table or text editor).
-
In general, the object background does not have
to be measured inside an annulus. The general rule is that the
optimum background value is the value at the coordinates of the
object centroid. In cases where the annulus would contain a bright
star, you may wish to manually calculate the background near the
object and use that to obtain the net count from the Ap Sum value. In this case, the following equation
gives the net count from an alternate background value:
|
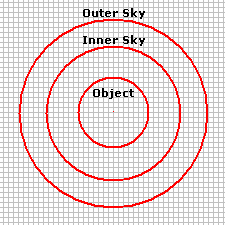
|
Diagram of a "measuring aperture" formed by an
object aperture and a sky sampling region between two outer
apertures.
The inner sky aperture should begin beyond the
light in the star profile. However, the sky measuring ring should
not be placed so far that it includes many other stars or that it
samples sky that is not the same as that underneath the object.
|
The inner, object measuring aperture can be adjusted to any radius
but, generally, it should not extend all the way to the point where
the star appears to merge into the sky noise as this will lower the
signal- to-noise ratio ("SNR") of the calculated magnitude. Use the
following guidelines to determine a reasonable size for the object
aperture:
-
The fraction of the object's total signal
measured by the object aperture must not change from one object to
another. This is accomplished by using apertures of the same
radius, ellipticity, and orientation for every object on all images
being measured together.
Note that the object aperture may be allowed to cut
onto the wings of the star profile. You can be totally safe by
making the object aperture large enough to contain "all the light",
but this adds more sky noise, which lowers the precision of the
measurement and makes the magnitude errors larger. On the other
hand, if the star profile varies over the region being measured,
you might use an object aperture large enough to hold all the light
for bright objects, or as the only option for measuring the field
of view.
The aperture photometry procedure uses 3 apertures
to measure the object. The central aperture measures the total
signal for the object while the local background is measure in the
annulus between the outer two apertures. The apertures may be
circular or elliptical, with any ellipticity and angle of rotation,
but all three apertures have the same shape and are concentric.
Elliptical apertures are used to measure objects when the Point
Spread Function ("PSF") is elongated by poor tracking or other
reasons. Matching the ellipse to the PSF shape gives a better
measurement by maximizing the signal through the aperture of a
given area, which in turn maximizes the signal to noise ratio.
Small Apertures
The general placement of a measuring aperture on the pixel grid is
shown below. In general, the object aperture, whether elliptical or
circular, or at whatever angle, will have partially sampled pixels
along its rim. For small apertures, a good measurement depends upon
correctly accounting for the partial pixel coverage. Mira properly
accounts for this case using a mathematically complex, but exact
partial pixel algorithm—the only one of its kind.
|
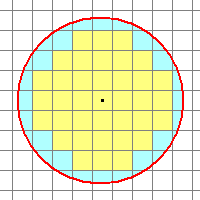
|
Enlarged view of the object aperture. The star's
light profile is assumed to extend outside the picture. so the
aperture does not contain all the light from the star. Many pixels
fall along the rim and are only partially measured by the
aperture.
Yellow: Fully sampled pixels.
Blue: Partially sampled pixels.
|
The Ellipticity parameter is defined
in terms of the axis ratio of the ellipse: for semimajor axis
a and semiminor axis b. The Ellipticity, e, is given
by
A circle has an ellipticity of 0. The major axis
orientation and the Radius are
adjustable using the Aperture Tool window. The orientation angle of the
semimajor axis is only used to determine how pixels are added to
the count sums. The ellipse properties that are independent of
angle are related to its size and ellipticity as follows:
All 3 apertures use the same radius, ellipticity,
and orientation for every measurement. If measuring an image set, Mira uses the same
properties for all images.
Calculating the Magnitude using an Alternative Background
When the background cannot be reliably determined
from pixels inside the background annulus, the Ap Sum value from the photometry output may be used
to calculate the magnitude. This procedure might be implemented
when the normal background annulus contains another object or a
region of bad pixels that cannot be rejected by the built-in
background method.
Before giving a procedure, let's look at how Mira
computes the Net Flux as described at
the beginning of this topic. The following equation uses the
photometry output quantitiesAp Sum and
Backgr . In addition, the object area
is calculated using the equation for Area A in the previous section. Remember that Mira
computes the value of Backgr using pixels inside the background
annulus:
This calculation is made internally using the
Object Area based on the aperture
properties specified in the Aperture Tool window. The Ap
Sum and Backgr are computed by
Mira and listed in the photometry output. The GAIN andEXPTIME keyword
values are applied to the Net Count to
calculate theNet Flux and thence the
magnitude ("Mag") listed in the
photometry output.
Calculating the magnitude using an alternative
background requires calculating two quantities:
-
The background value estimated by some means and
evaluated at the centroid of the object;
-
The aperture area as calculated using the
Area equation above.
The alternative background can be estimated in
numerous ways. The background value may be estimated at the
Image Cursor
location using the method described in the Statistics
Measurements topic. The estimator is chosen or configured using
the Statistics
Properties dialog. Since the optimal background is evaluated at
the position of the object, obtaining the background value may
involve averaging estimators obtained symmetrically on opposite
sides of the object. Let the value Alt
Bg be the alternative background value calculated in some
way. Then the following equation gives the Net Count:
The Net Flux and
Magnitude may then be calculated from
the Net Count. This can be calculated
by hand, a spreadsheet, or a Mira script.
Using a Script to Implement an Alternative Background
A Mira script may be implemented to automate the
process of utilizing an alternative background. The script would be
called from the photometry measurements grid. Here is an outline
for creating such a script:
-
Read the Ap Sum
column from the measurements table to get the total count inside
the object aperture
-
Compute the background, Alt
Bg, from pixels in one or more background regions nearby or
surrounding the target object:
-
-
Evaluate the background at the location of the
object. This gives the value Alt
Bg.
-
Calculate the aperture area using the equation
above with aperture properties from the photometry
configuration.
-
Apply the equations above to calculate the
Net Flux and Magnitude
-
Photometric errors may be calculated as in
Photometric Error Definitions.
Related Topics
Aperture Photometry
Photometric Measurement Definitions
Photometric Error Definitions
Mira Pro x64 8.72 User's Guide, Copyright Ⓒ 2024 Mirametrics, Inc.
All Rights Reserved.

